Блог про HR-аналитику: Изучаем регрессию дальше

понедельник, 14 августа 2017 г.

Изучаем регрессию дальше

Задача

В предыдущей статье «Регрессия: Как начать предсказывать» мы коснулись темы простой линейной регрессии. Сегодня мы продолжим погружаться в эту интересную тему.

Итак, задача на сегодня у нас следующая. Есть данные участников мастер-класса по скорочтению (126 наблюдений). Мы построим модель прогноза Количества прочитанных книг за год на основании Скорости чтения человека. Т.е. Количество книг это зависимая переменная, а Скорость чтения – это независимая переменная (предиктор).

В предыдущей статье мы уже строили простую линейную регрессию.

В этой статье мы задействуем следующие методы:

· Полиномиальная регрессия

· Decision Tree («Дерево решений»)

· Random Forest («Случайный лес»)

· SVR (метод опорных векторов)

· KNN (метод k-ближайших соседей)

После того как мы построим все эти модели, мы их протестируем на тестовой выборке. И после этого посмотрим, какая модель лучше всего справилась с заданием. Т.е. выберем лучшую.

Подготовка данных

У нас есть набор данных участников мастер-классов по скорочтению. База, на основании которой мы будем строить нашу модель.

Загрузить данные в R можно следующей командой:

dataset <- read.csv("SpeedReading_4_Groups.csv", sep = ";")

Посмотреть на первые шесть строк нашего датасета можно так:

head(dataset)

Никакой особой подготовки или преобразований наши данные не требуют.

Нам только нужно разделить наши данные на тренировочный и тестовый наборы данных. Т.е. на тренировочном датасете мы будем тренировать наши модели, а на тестовом – будем их тестировать.

Разделить наши данные на два датасета можно следующим кодом:

trindex = sample(1:nrow(dataset), nrow(dataset)*0.8)

training_set = dataset [trindex, ]

test_set = dataset [-trindex, ]

В результате такой операции мы получим два датасета:

training_set – тренировочные данные

test_set – тестовые данные

При этом данные будут распределены в пропорции 4/5. Т.е. 80% данных пойдет в тренировочные датасет, а 20% оставшихся в тестовый.

Вспоминаем линейную регрессию

Давайте построим простую линейную регрессию с одной независимой переменной, как мы это делали в прошлой статье.

У нас получится следующая модель:

А также давайте визуализируем данную модель.

Линейные модели мы можем использовать, когда выполняются определенные условия. Такие, как, например, линейная взаимосвязь и нормальное распределение наших переменных.

Тест на нормальность распределения наших переменных:

А также гистограммы:

Т.е. наша зависима переменная (Количество прочитанных книг) не прошла тест на нормальность. Кроме того, если посмотреть на график scatter plot, где отображена взаимосвязь наших двух переменных, то мы увидим, что связаны они не совсем линейно.

Нелинейные модели

Теперь давайте попробуем решить нашу задачку при помощи нелинейных моделей.

Полиномиальная модель

Построить такую модель совсем несложно. Достаточно добавить несколько полиномов. Например, это можно сделать так:

training_set$Level2 = training_set$Скорость.чтения^2

training_set$Level3 = training_set$Скорость.чтения^3

training_set$Level4 = training_set$Скорость.чтения^4

poly_reg = lm(Сколько.книг~Скорость.чтения+Level2+Level3+Level4, data = training_set)

summary(poly_reg)

В результате выполнения данных команд мы получим следующую модель:

Интерпретация такой модели ничем не отличается от линейной модели. Здесь мы можем увидеть все предикторы, а также посмотреть чему равняется R² нашей модели.

Давайте визуализируем и данную модель:

Теперь давайте построим и другие типы моделей.

· Decision Tree («Дерево решений»)

· Random Forest («Случайный лес»)

· SVR (Метод опорных векторов)

· KNN (Метод k-ближайшего соседа)

У данных методов есть настраиваемые параметры. В данной статье мы не будем детально вдаваться во все подробности такой настройки, а попробуем использовать некие “стандартные” величины.

Decision Tree («Дерево решений»)

Для построения модели Decision Tree достаточно выполнить следующий код:

dTree <- rpart(formula = Сколько.книг ~ Скорость.чтения,

data = training_set,

control = rpart.control(minsplit = 3))

И давайте также визуализируем полученный результат:

Мы видим, что данный метод совсем по-другому визуально пытается описать наши данные в отличие от простой линейной регрессии.

Random Forest («Случайный лес»)

Двигаемся дальше. Теперь метод Random Forest. Для построения регрессионной модели данным методом необходимо выполнить следующий код:

rndForest = randomForest(x = training_set[5],

y = training_set$Сколько.книг,

ntree = 5)

И давайте посмотрим на визуализацию нашей новой модели:

Из рисунка видно, что данный метод еще более «изощрённо» пытается описать наши данные.

SVR (Метод опорных векторов)

Переходим к следующему методу – SVR (Метод опорных векторов). Для построения регрессионной модели, необходимо выполнить следующую строку кода:

fitSVM = svm(formula = Сколько.книг ~ Скорость.чтения,

data = training_set,

type = 'eps-regression',

kernel = 'radial')

И также давайте посмотрим на графическое отображение нашей новой модели:

Рисунок показывает нам, что данный метод строит более плавную линию для описания наших данных.

KNN (Метод k-ближайшего соседа)

И последний метод k-ближайшего соседа. Для построения регрессионной модели при помощи данного метода, нам необходимо выполнить следующий код:

fitKNN <- knn.reg(training_set[5], test_set[5], training_set[,4], k = 5)

И визуализируем нашу модель на графике:

Из рисунка мы видим, что метод KNN чем-то похож на визуализацию Random Forest. Такая же ломанная кривая линия.

Тестируем и выбираем лучшую модель

Теперь давайте протестируем все наши 6 моделей на тестовом наборе данных. Если помните в самом начале мы разделили наш датасет на две части: тренировочный датасет и тестовый датасет. До этого момента мы использовали тренировочный датасет. А теперь мы воспользуемся тестовыми данными.

Т.е. ответим на вопрос, а какая модель лучше других может более точно предсказывать значения Количества прочитанных книг на новых данных.

В этом нам помогут три показателя:

MAE (Mean Absolute Error) – Средняя абсолютная ошибка между предсказанной и реальной величиной. Чем меньше ошибка, тем лучше.

RMSE (Root Mean Squared Error) – Квадратный корень из среднеквадратичной ошибки между предсказанной и реальной величиной. От МАЕ отличается тем, что «штрафует» большие ошибки сильнее. Чем меньше, тем лучше.

Rsq (коэффициент детерминации) – это доля дисперсии зависимой переменной, объяснённая нашей независимой переменной или переменными. Чем он больше, тем лучше.

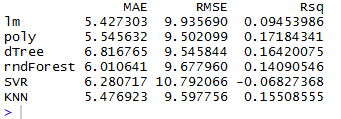
После несложных вычислений и применения наших 6-ти моделей к тестовым данным, мы получим вот такую таблицу:

Давайте выберем трех лидеров по каждому показателю:

МАЕ: линейная, KNN и полиномиальная

RMSE: полиномиальная, Decision Tree и KNN

Rsq: полиномиальная, Decision Tree и KNN

По всем трем показателям у нас лидируют две модели: полиномиальная и KNN.

Ранее я говорил о том, что метод KNN-регрессии имеет настраиваемый параметр. Этот параметр (k) задается в формуле. Когда мы строили модель первый раз, мы задали стандартное значение 5. Но давайте теперь попробуем подобрать оптимальное значение (k), при котором наша ошибка RMSE будет минимальной.

Запустив совсем несложный цикл, мы получим следующий результат:

Т.е. наша ошибка RMSE будет минимальной при k=3. Давайте еще раз построим модель KNN с учетом нового значения k=3.

fitKNN <- knn.reg(training_set[5], test_set[5], training_set[,4], k = 3)

И теперь еще раз рассчитаем все наши параметры для выбора лучшей модели:

Мы видим, что настройка параметра k дала свои результаты. Теперь у нас у метода KNN самая минимальная ошибка RMSE и самый большой Rsq.

Мы могли бы тюнинговать и другие методы, но это уже материал для новой статьи.

Теперь визуализируем все наши модели (линии) и на эти же графики точками нанесем данные из тестового датасета. Так мы сможем понаблюдать воочию, насколько точно наши модели описывали новые данные.

Ниже представлен именно такой график: